The Kelly criterion is a mythical creature.
On the one hand, it’s a very basic mathematical concept offering great things (and fortunes) to those who understand it. But on the other hand, it’s hardly included in any textbooks in economics, investing, or, for that matter, portfolio management. To my knowledge, the concept is not in the entire CFA program and I never encountered it during my time in business school.
Yet, the Kelly criterion is adopted by some of the best concentrated investors in the world and the mathematics behind it is irrefutable. Then why isn’t it more supported within academic circles of economics?
The answer, I believe, is two-fold. First, it was invented by an information theorist, not an economist, and for that reason, economists reflexively defend their turf. Second, there’s an over-emphasis on volatility-adjusted returns (I purposely did not write risk-adjusted returns here) and widespread preaching of diversification going on in business schools. The Kelly criterion finds no place here because it doesn’t offer you a way to maximize your volatility-adjusted returns but instead offers you a way to maximize the growth rate of your wealth.
It’s interesting because the Kelly criterion was developed around the same time as modern portfolio theory. But while the Kelly criterion requires an estimate of the probability distribution of investment outcomes ahead of time, modern portfolio theory measures the risk of investments based on their past variances. This is why Markowitz’s mean-variance optimization is getting all the limelight. The Kelly criterion is too simple and suggests an inefficient market.
Now, for any bottom-up investor—as any serious long-term value investor is—mean-variance optimization is a fool’s errand because the natural path of a bottom-up approach is towards a concentrated investment portfolio of mispriced securities. Yes, you can optimize through covariance between assets held in a concentrated portfolio to a degree, but you first and foremost want to make sure that the hard work you put into picking a few stocks will be well-rewarded through adequate position sizing so that your best bets reap the greatest returns. This is where the Kelly criterion should dominate.
In this article, I explain how I think you should properly use the Kelly criterion as applied to long-term value investing. But before I do that, there are two mental models that are vital to know before you can fully appreciate what the Kelly criterion has to offer and what it doesn’t have to offer.
Thus, this article is split into two sections.
In the first section, I introduce the mental model of gambler’s ruin and the mental model of leverage. Now, you may already think that you fully understand what leverage is, but perhaps you might learn something new about how it affects wealth when it’s applied correctly and when it’s applied detrimentally, especially over the long term and to sequential bets. The default thinking about leverage is in the short term. You’ll learn how to take a long-term view.
In the second section, I discuss how the Kelly criterion works. I then take what we’ve learned and apply that to the game of long-term value investing focused on concentrated bets. I discuss the dangers that may come from naively trusting the Kelly criterion’s suggestions and propose a practical solution. This practical solution is fully in line with how I invest at Junto.
The Mental Model of Gambler’s Ruin
Professional betting—whether gambling, investing, or handicapping—is about having an advantage with a positive expected return. If you don’t have any statistical edge, you shouldn’t bet at all. But having a statistical edge is only one part of the equation. The other part of the equation is the delicate issue of bet sizing (or “money management”). And I believe this other part is more delicate and critical than you think.
In fact, you can be the world’s greatest handicapper, but if you can’t manage your money, you’ll end up either broke or way below the potential of your hard work. And the sad fact is that almost any gambler who has an edge but disregards money management goes broke in the long run.
Of course, this requires an explanation.
Let’s say you have an equal bet in which the odds of you winning or losing is 50% and the house takes nothing. You continuously bet a fixed dollar amount in each bet. In such a bet, the mathematical expectation of your wealth change is equal to zero. You are just as likely to win as you are to lose and the statistics say that your wealth should move in a horizontal line.
And often when we think about future expectations, we rely on such statistics. But that is, of course, pure fantasy. In reality, your wealth path would not move in a horizontal line. In reality, your wealth would follow a random walk that gets increasingly chaotic over time.
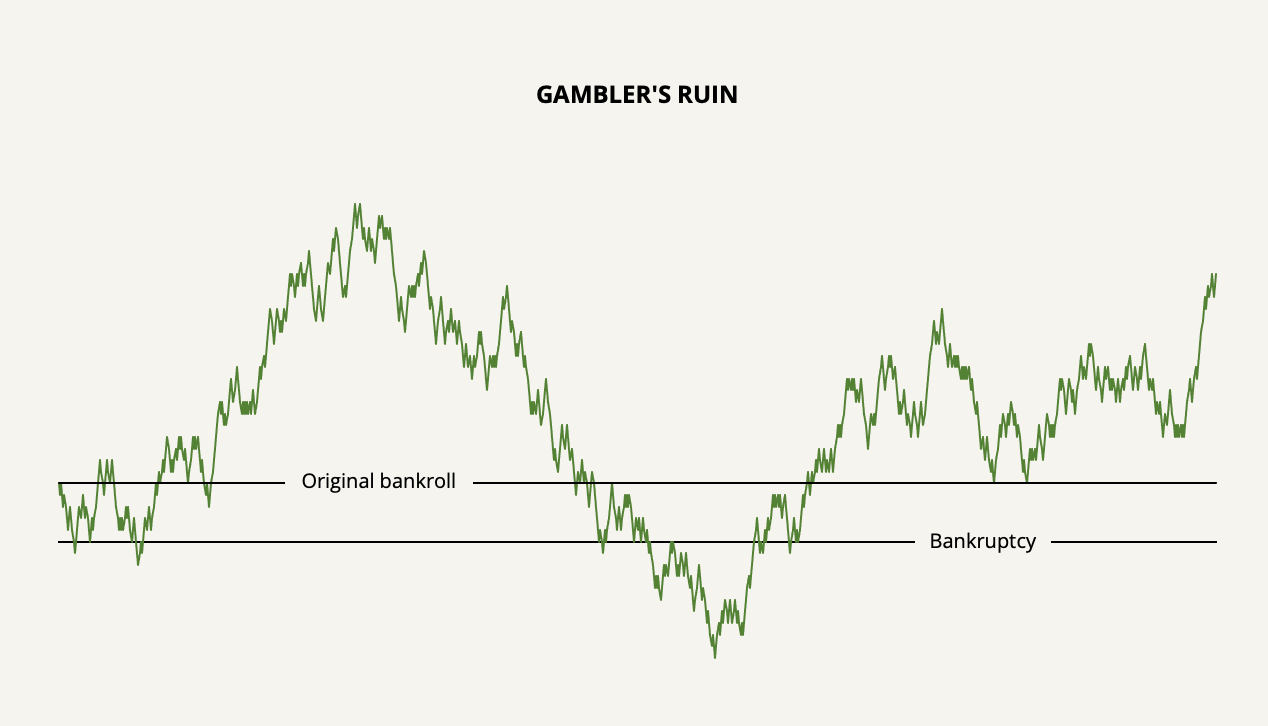
If we were to extend the wealth line into infinity, it would cross your original bankroll an infinite number of times. You would also go broke an infinite number of times. But this is irrelevant since you can only go broke once and then you’re out of the game. And notice how early bankruptcy happens.
If you were to play a negative expected-return game such as in a casino, the path to bankruptcy would happen even faster. And even if we were to give a small statistical edge such as a 51% win rate, it’s still possible for a persistent gambler to go broke at some point. This is the gambler’s ruin problem.
Knowing this, consider now the foolish betting strategy by the name of martingale. This is the strategy in which you double up your bet every time you lose until you win. Of course, the effect of the martingale system is that it accelerates the gambler’s ruin problem.
The solution to gambler’s ruin—as I think you’ve already figured out—is to bet bankroll proportions instead of fixed dollar amounts so that you bet more as your bankroll increases and you bet less as your bankroll decreases. But even doing that doesn’t shield you from gambler’s ruin if your betting proportions are too aggressive for your statistical edge.
So now the question becomes: How much of the bankroll should you bet? Is there an optimal bet size that assures you to never fall prey to gambler’s ruin while maximizing your long-term wealth?
The Mental Model of Leverage
Leverage has counteracting forces: It either amplifies your gain or amplifies your loss. Almost everyone understands that.
But not everyone understands how these counteracting forces come into play when applied over longer time periods and through multiple bets, even as these bets have positive expected returns.
To explain, let’s take an example.
Say you have a rigged coin-tossing game in which the coin is designed so that it lands on heads 51% of the time and lands on tails 49% of the time. The payoff is even. You are well aware of the coin’s design and you know that the probabilities are in your favor. You now also know that you must bet bankroll proportions to avoid gambler’s ruin.
Let’s first see what might happen to your wealth over time if you continuously bet 1%, 2%, or 5% of your bankroll on heads 1,000 times.
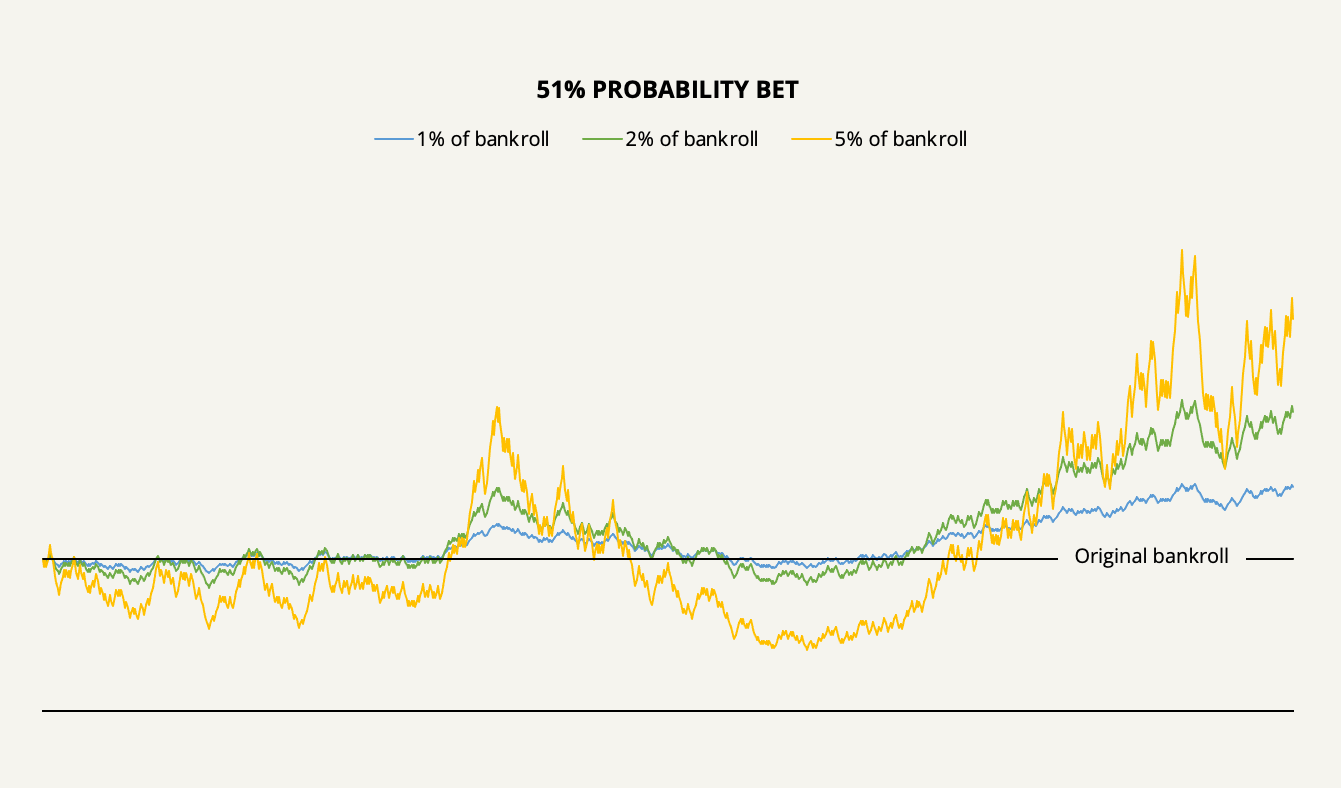
With a 1% betting strategy, the simulation shows that you could have made a return of 47.7% of your original bankroll with mild volatility. You could also have made a higher return, albeit more volatile, with larger bet sizes. This is the intuitive way to think about leverage.
Now, let’s look at the counter-intuitive reality of what happens when we increase your bet size even more, say to 10%, 15%, or 30% of the bankroll with each bet.
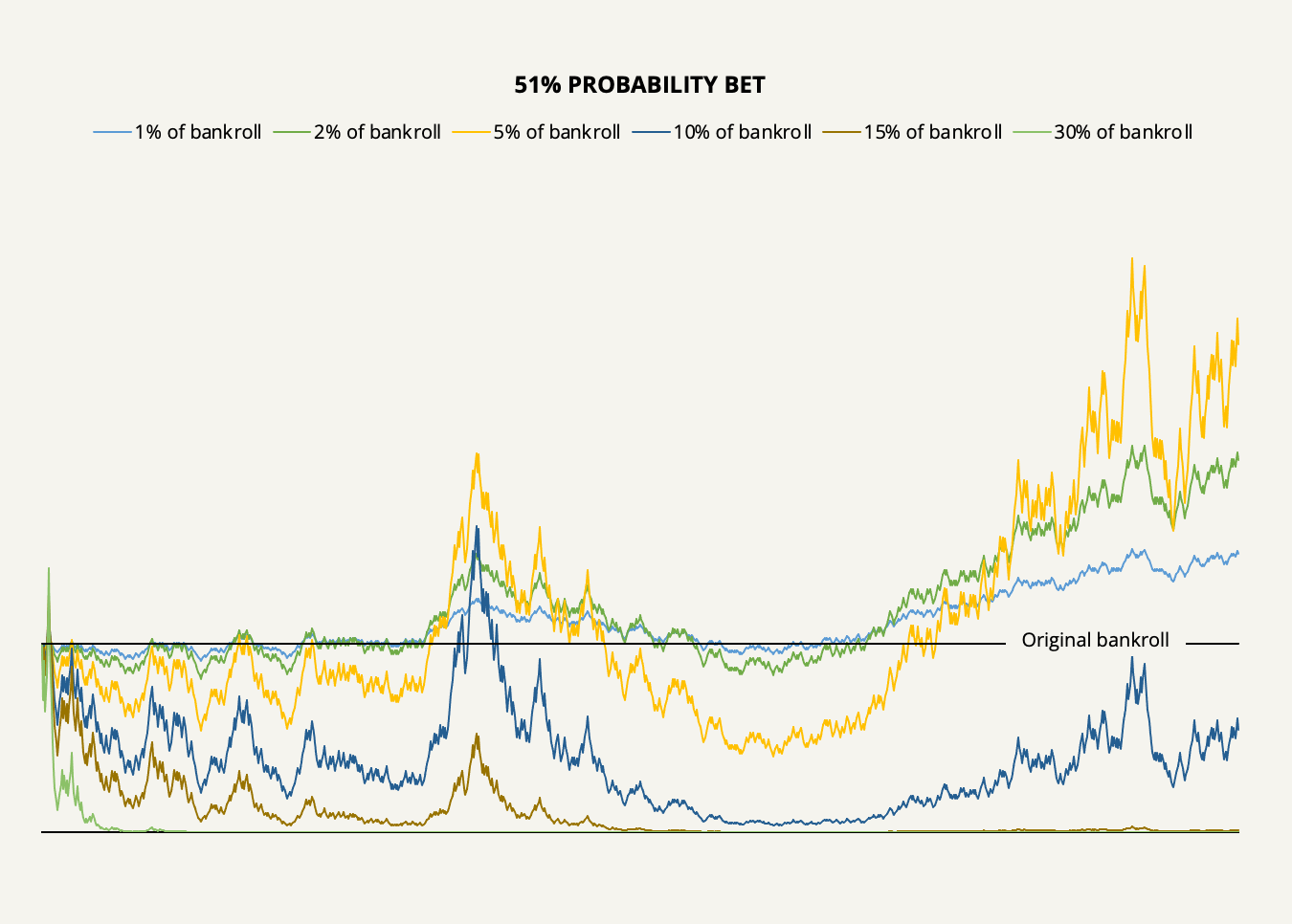
As our simulation shows, it’s easy to lose money, even with a mathematical advantage. Increasing your bet sizes too much will devastate your bankroll: With a 10% betting strategy, you would only have half of your bankroll left, and with 15% and 30%, your bankroll would essentially be ruined.
Think about what’s going on for a minute. With a 5% bet size or 2% bet size (which, as we’ll later find, is the long-run optimal), your bankroll would increase faster than a 1% bet size. But with a 30% bet size, it would lead to fast ruin. In the first case, leverage is obviously helping, and in the second case, it’s detrimental.
Why is that?
The reason is that at a very specific point, the marginal profit you earn from adding more leverage shrinks and eventually turns negative. To further explain, let’s switch our example around to an equal probability bet but with unequal payoffs and which requires actual leverage in the terms of borrowed money.
Say you have an investment opportunity that is 50% likely to work out. If it does, you will earn a 20% return on your investment, and if it doesn’t, you will lose 10% of your investment. The payoff ratio is therefore 2-for-1 and the reason why we can now borrow money to amplify our return is that risking 100% of our capital can only lead to a loss of 10%.
Now, instead of doing a 1,000-bet simulation, let’s only do two successive bets: one win and one loss (the order doesn’t matter). Then we can iterate using different levels of leverage.
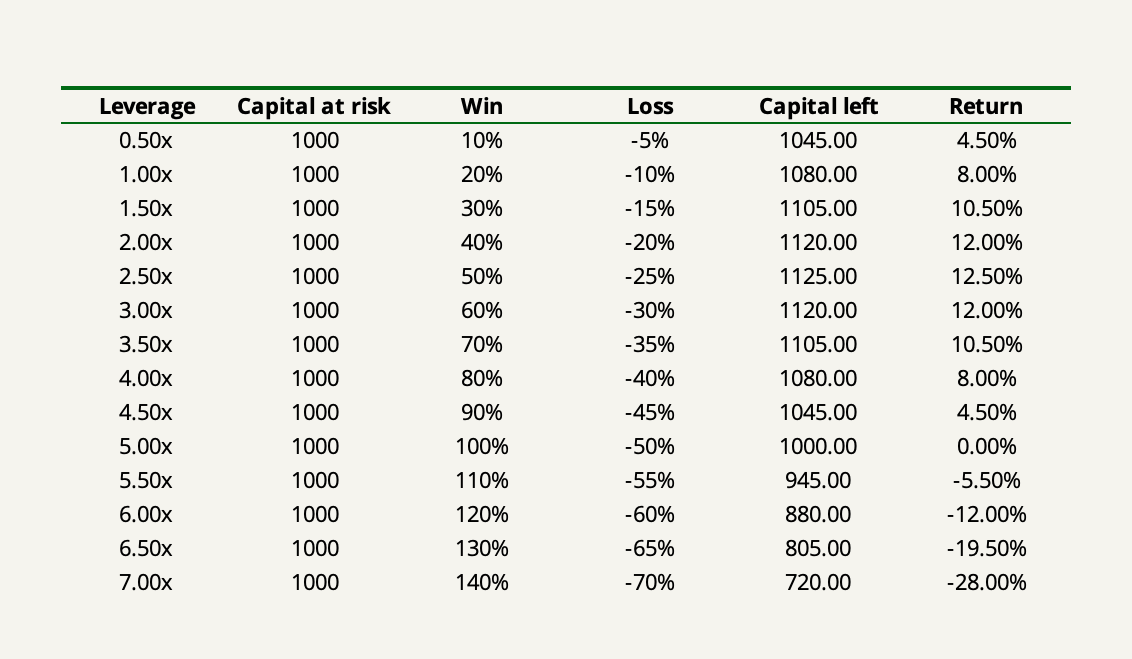
What we see is that as soon as the leverage exceeds 2.5x, the return made from the two bets starts to drop off and eventually goes negative at over 5x leverage.
The reason why this happens is that the loss incurred on the second bet more than offsets the return made on the first since that loss is taken from a larger pool of capital. It’s the same geometric effect as if you gain 10% on an investment and then lose 10%, you’re one percent down on your original investment.
It’s when this marginal geometric effect exactly offsets the marginal benefit of adding more leverage that you have the optimal level of leverage. In this case, the leverage that maximizes your return is exactly 2.5x.
Now that we understand the mental models of gambler’s ruin and leverage, we are ready to move on to the Kelly criterion.
The Kelly Criterion Explained
The beautifully simple formula for the Kelly criterion calculates the optimal proportion of your bankroll to bet in order to maximize the geometric growth rate of your wealth. But not only does it promise you maximum profit from effectively leveraging your opportunities; it also promises you safety from gambler’s ruin.

f is the proportion of your bankroll that you should bet which is the function of the probability of winning, the probability of losing, and the odds you have—i.e. the payoff ratio.
The Kelly criterion has three prerequisites:
- You must know the exact odds and probabilities to input.
- If only one of them is in your favor, it must more than offset the other, i.e. there must be a positive expected return.
- You must scale the Kelly output so that the amount you bet is equal to the potential loss.
The last point is vital and it’s where I see a lot of people go wrong when using the formula. I’ve found many websites that don’t scale the output correctly when dealing with a situation where you can lose “some” but not all. It’s amazing how far up the academic ladder this goes. Seeing how so many practitioners of the Kelly criterion get this wrong brings home a quote of Ed Thorp’s from his early days in the stock market that he was both surprised and encouraged at how little was known by so many.
The Kelly criterion must be used in such a way that what is bet must equal the potential loss. It’s inherent in the word “bet”: What we bet is what we put on the line. In our leveraged investment example, the base loss was 10%, so if we were to put 100% of our capital into the bet, we could only lose 10%. Thus, the right thing to do in this case is to scale the output by 10 which leads to a leveraged bet.
Let’s take our examples so far and put them into the Kelly formula.
In the rigged coin-tossing game we had a 51% win probability with equal payoffs. Inserting these inputs in the Kelly criterion formula shows that the optimal betting proportion of our bankroll is 2%.
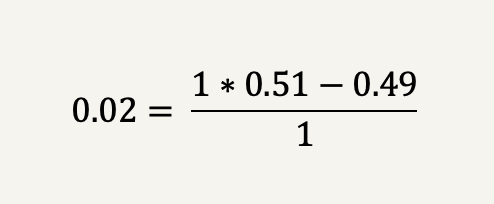
In our investment example, we had a 50% win probability with unequal payoffs of 2-for-1 (20% win vs. -10% loss). The Kelly criterion, therefore, suggests betting with a maximum loss of 25% of the bankroll which, as we found out, is equal to a 2.5x leverage from the base loss of 10%.
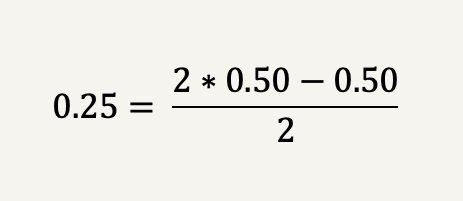
Let’s take a more normal investment example that wouldn’t require leverage in the terms of borrowed money. Say you found a company that you believe is worth at least $100 dollars per share and it’s currently trading at $80 per share. You are only 50% certain that the company is worth your intrinsic value estimate.
The odds in this case is 1.25 (100 divided by 80) and the Kelly criterion thus suggests to bet 10% of the bankroll on the investment.
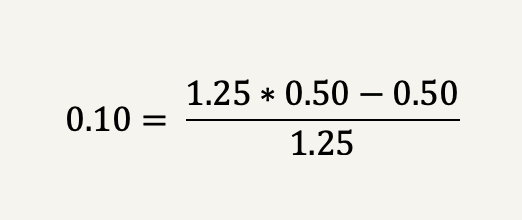
It all looks plain and simple. But what if we dive a bit more into the engine?
Think about the fact that the Kelly criterion promises you maximum profit while protecting you from ruin. Such promises may sound antithetical. But the root idea behind the Kelly criterion is that there is a tradeoff between risk and return which we can present as the Kelly curve.
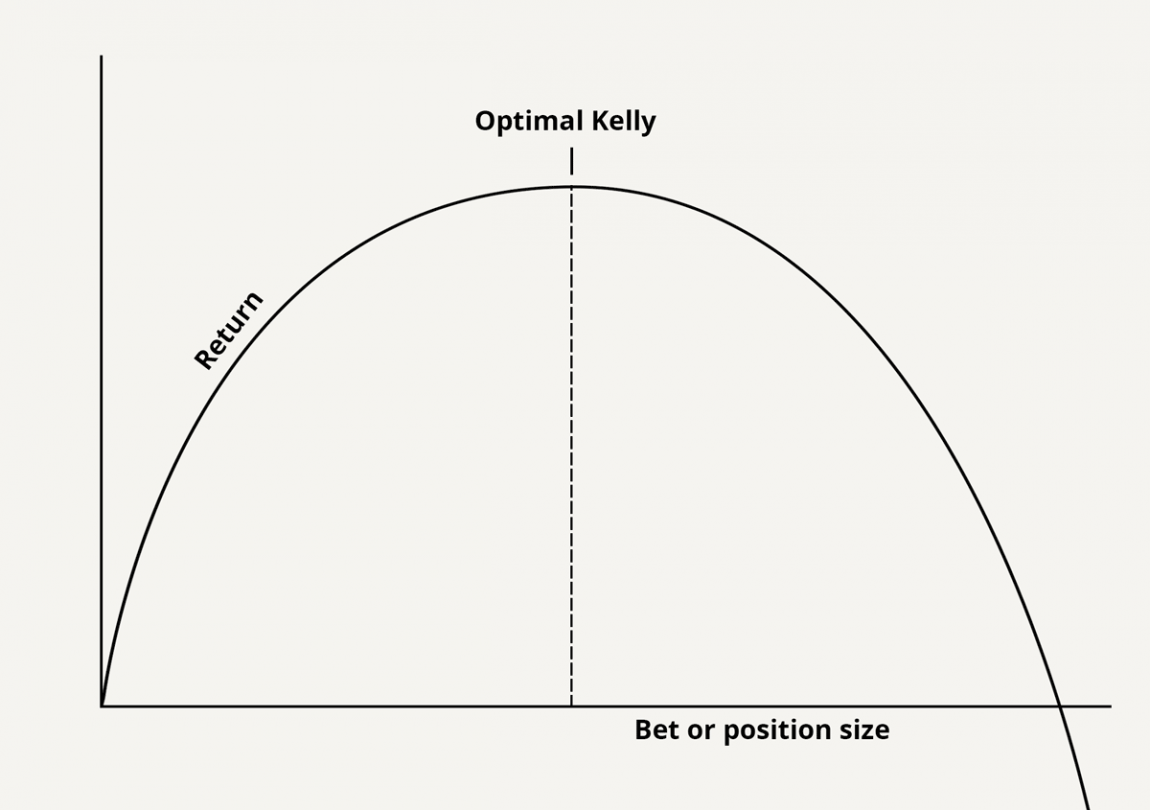
Now, I want you to notice two things.
First, notice how near the top the increased return you get from adding extra risk becomes tiny. In fact, as the bet size approaches the top, the ratio of marginal risk to marginal profit goes to infinity. Eventually, you would have to risk an additional one billion dollars to earn one more cent of expected profit. The reason is that the Kelly criterion assumes no value is placed on risk as long as it maximizes the return.
Second, notice that betting just a tiny bit more than the Kelly criterion suggests leads to decreased profits with higher risk (which we already know that from the mental model of leverage).
What this means is that the goal is not necessarily to pick the exact top of the Kelly curve. First and foremost, the goal is to stay within the left side. The left side represents rationality while the right side represents irrationality, or insanity.
Let’s see what might happen if we were to underbet or overbet the Kelly criterion’s suggestion using our unequal payoff example in a 100-bet simulation.
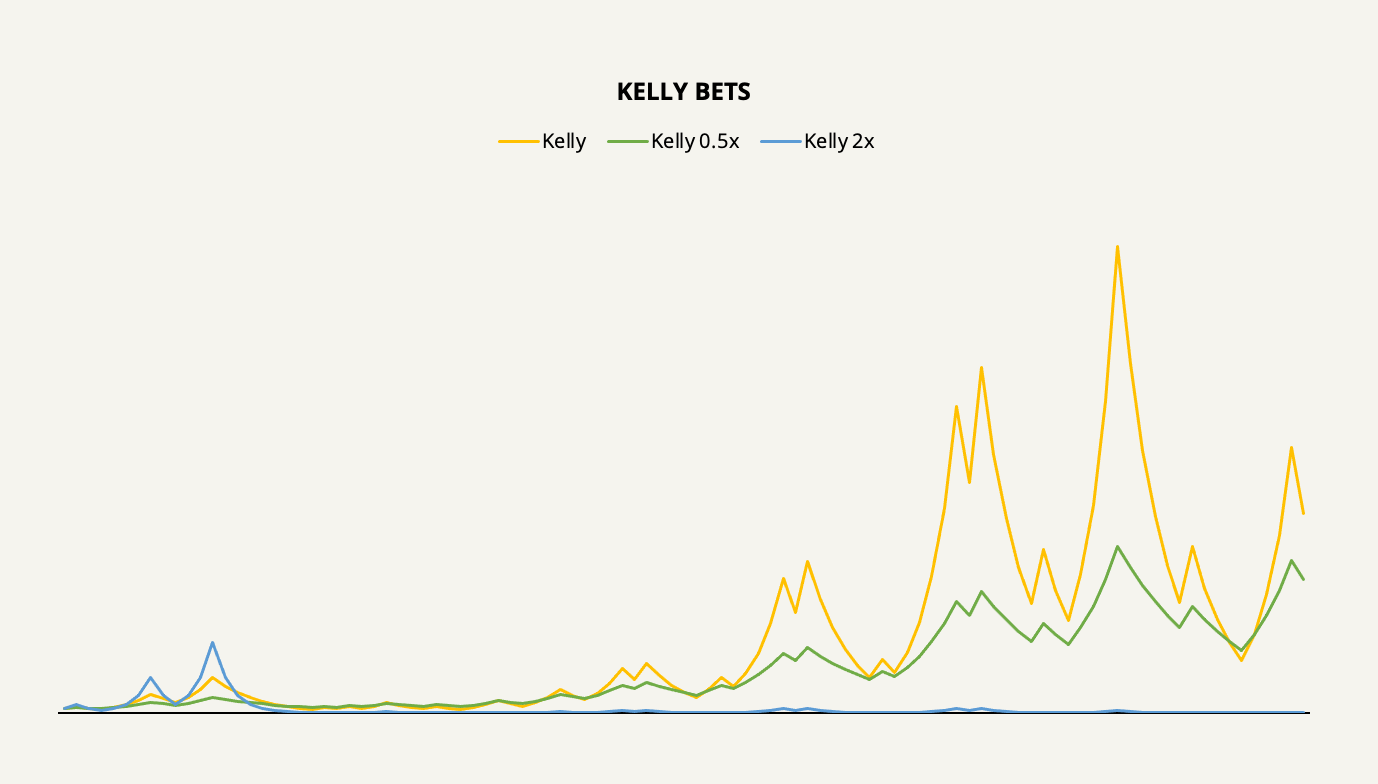
Consistent with the two-bet example, the Kelly-optimal betting size, of course, leads to a significantly higher return in the long run as compared to underbetting or overbetting. The longer we stretch out the time horizon, the bigger this difference is going to get by compound interest.
Does this mean that we should always try and stretch for the Kelly optimal point as long as we’re on the left side of the curve? No, it doesn’t. In the vast majority of cases, especially in investing, it actually makes sense to err on the side of caution and underbetting may be the right strategy in the long run. To understand why that is, we can now introduce another mental model by the name of “law of large numbers”.
The Kelly Criterion Applied to Long-Term Value Investing
There is one—often overlooked—catch to investing: Life is short and opportunities don’t come around often. In games such as our coin-tossing example, you could either double or lose your bet every few seconds. In investing, doubling your money takes years.
The problem is that this nature of investing goes against the real engine behind the Kelly criterion: the law of large numbers. Ever since it was proved by Jakob Bernoulli in 1713, this law has caused a lot of confusion with gamblers (and investors).
In American roulette, there’s an 18/38 chance that the ball lands on red in any game played. But if you were to play the game of roulette 38 times in a row, you, of course, wouldn’t expect the ball to land on red exactly 18 times. Likewise, if you were to play the game 38 million times, you would in no way expect it to land on red 18 million times. No matter how many times you play, there’s never any certainty of achieving the expected number of reds. But as the number of games is increased you can expect one thing: that the percentage of reds landed will tend to come closer to the expected percentage. This is the law of large numbers.
Investing isn’t a casino game and you won’t have many sequential bets. Therefore, absent a certain fulfillment of the law of large numbers, the Kelly criterion may involve more short-term risk than you might be prepared to take.
This has another effect: You can only pick the opportunities in which you have a significant edge. (A winning probability of 51% in a coin-tossing game isn’t worth much if you can only do one bet.) Of course, the natural effect of this is towards a concentrated portfolio.
But how concentrated?
It really depends on your ability to estimate probabilities and correctly value companies. The stock market is not a controlled environment where odds are static and given in advance. The odds are fluid, they change daily, and it’s difficult to get enough of an edge to actually make a bet.
I propose a four-fold solution to these problems:
- Be conservative in your intrinsic value estimate (which determines your odds) and your level of confidence in the estimate (which determines your probability).
- Apply at least a 20% margin of safety to the Kelly criterion’s suggestion.
- Invest only in companies where there’s at least a 70% probability of you being right in your valuation.
- Treat the Kelly criterion as a thought experiment rather than a mechanical exercise.
The first point mitigates the fact that in valuing companies, overconfidence is pretty much always a factor, and reality will almost always turn out less profitable than expected.
The second point provides an appealing trade-off. Only betting fractions of the Kelly criterion limits the probability of drawdowns by an exponential factor. For example, when you apply a 50% margin of safety (only betting half of the Kelly criterion’s suggestion), you end up with 75% of the optimal profit while your risk is reduced by half.
The third point ensures that you keep within your circle of competence—which is the most important point in this entire discussion.
And lastly, the fourth point urges you not to try and calculate the Kelly criterion’s suggestion for everything. Trying to pin down an exact position size can blind you from the dynamic nature of investing and valuation. When your edge is large enough, you will know to bet big.
The Kelly criterion is a mental model in itself that brings great rewards to those who understand how to use it and how not to use it. For you to reap the benefits of the Kelly criterion, you must stay in the game long enough for the law of large numbers to start to work. This four-fold solution is your surefire ticket.


