Picking great stocks isn’t the same thing as picking great companies.
The investing game would be a whole lot easier if that was the case. In such a game, success would simply require picking the companies with the strongest fundamentals and wait for the stock price to rise with the business. But that isn’t how the stock market works.
In reality, a great company with a significant competitive advantage can turn out a poor investment because fundamentals are only one part of the investing problem.
And in reality, the most boring companies—candy, consumer staples, tools—can make some of the best long-term investments while the most innovative can make some of the worst.
To understand why, two mental models come in handy.
Mental Model: Pari-Mutuel Systems
In his famous speech, “The Art of Stock Picking”, Charlie Munger points out that pari-mutuel systems are a great mental model to think about the nature of the stock market.
Pari-mutuel systems are ones in which all bets of a particular type are placed together in one pool, the house takes a cut off the top, and the payoff odds are calculated by sharing the pool among all winning bets. In other words, the odds change based on what’s bet. This system differs from fixed-odds bets in which the payout is agreed upon at the time the bet is sold.
Horce racing is a pari-mutuel system. Bettors go to the racetrack, bet on their favorite horse, and the potential payoff for the most popular horse goes down while the payoff for the least favorite goes up.
Charlie Munger writes:
Any damn fool can see that a horse carrying a light weight with a wonderful win rate and a good post position etc., etc. is way more likely to win than a horse with a terrible record and extra weight and so on and so on. But if you look at the odds, the bad horse pays 100 to 1, whereas the good horse pays 3 to 2. Then it’s not clear which is statistically the best bet using the mathematics of Fermat and Pascal. The prices have changed in such a way that it’s very hard to beat the system.
And then the track is taking 17% off the top. So not only do you have to outwit all the other betters, but you’ve got to outwit them by such a big margin that on average, you can afford to take 17% of your gross bets off the top and give it to the house before the rest of your money can be put to work.
The stock market works the same way, except the house take is minuscule compared to horse racing. What you pay by participating in the stock market is the commission and spread which is usually less than one percent.
Then the question comes to efficiency. Is the market inefficient enough for a shrewd market participant to outwit all the other participants and still be able to afford the trading fee on every trade? Like horse racing, the stock market is efficient, but it’s only partly efficient.
You can essentially outwit other market participants in three ways: You can either have more information, be more intelligent, or have a better temperament. The first one seems either unlikely or potentially illegal given the internet age’s flow of information. The second two are what you rely on.
So how intelligent do you need to be? Charlie Munger writes:
Intelligence should give some edge, because lots of people who don’t know anything go out and bet lucky numbers and so forth. Therefore, somebody who really thinks about nothing but horse performance and is shrewd and mathematical could have a very considerable edge, in the absence of the frictional cost caused by the house take.
But temperament carries the most freight.
[…] the one thing that all those winning betters in the whole history of people who’ve beaten the pari-mutuel system have is quite simple. They bet very seldom.
It’s not given to human beings to have such talent that they can just know everything about everything all the time. But it is given to human beings who work hard at it ‑ who look and sift the world for a mispriced be that they can occasionally find one.
And the wise ones bet heavily when the world offers them that opportunity. They bet big when they have the odds. And the rest of the time, they don’t. It’s just that simple.
That is a very simple concept. And to me it’s obviously right based on experience not only from pari-mutuel systems, but everywhere else.
When operating in pari-mutuel systems, the trick is to seek and find those rare opportunities in which the odds aren’t commensurate with the payoff ratios. The bets with the highest likelihood of winning can either be a very good bet or a very bad bet, and the difference between the two is determined by the odds—the price you pay for the investment.
But here’s the catch: In order for you to buy a cheap company with great odds, the pari-mutuel system says that this company must be unpopular. You must have a conviction about the company that other market participants don’t.
Companies become unpopular for a reason. It may be due to issues such as mounting losses, a declining market share, a shrinking addressable market, a high level of debt, or other characteristics that to one investor may seem like a factor of continued poor performance while it to you may look like “temporary trouble”.
In other words, you can have cheap stock prices and you can have good news, but you rarely have both at the same time. Investing is an arrogant act; For you to make an investment, you are effectively saying that you have an advantage over the seller and other market participants.
So you have to be sure of your conviction in order to play pari-mutuel systems right. And the only way to do that is by staying within your circle of competence. If you stray outside of your circle of competence, you can in no way expect to determine the right odds better than the other person and you have no edge in pari-mutuel systems.
Mental Model: Knightian Uncertainty
Any investment you make involves certain levels of risk and uncertainty. Oftentimes, the two concepts are used interchangeably. But that is a mistake. There’s a big difference between risk and uncertainty and it was first distinguished by University of Chicago economist Frank Knight in 1921.
For example, if you roll two dices a million times, the law of large numbers says that there’s a good probability that the dices will land a two 2.78% of the times and that they will land a seven 16.67% of the times. This is a certain system.
In another case, it’s very difficult to assess the future outcome of the 10-year interest rate and the big macro picture ten years, or even one year, into the future. This is an uncertain system.
In the real world, forecasting events will fall somewhere between these two extremes.
The difference between a certain event and an uncertain event lies in the ability to determine its probability distribution.
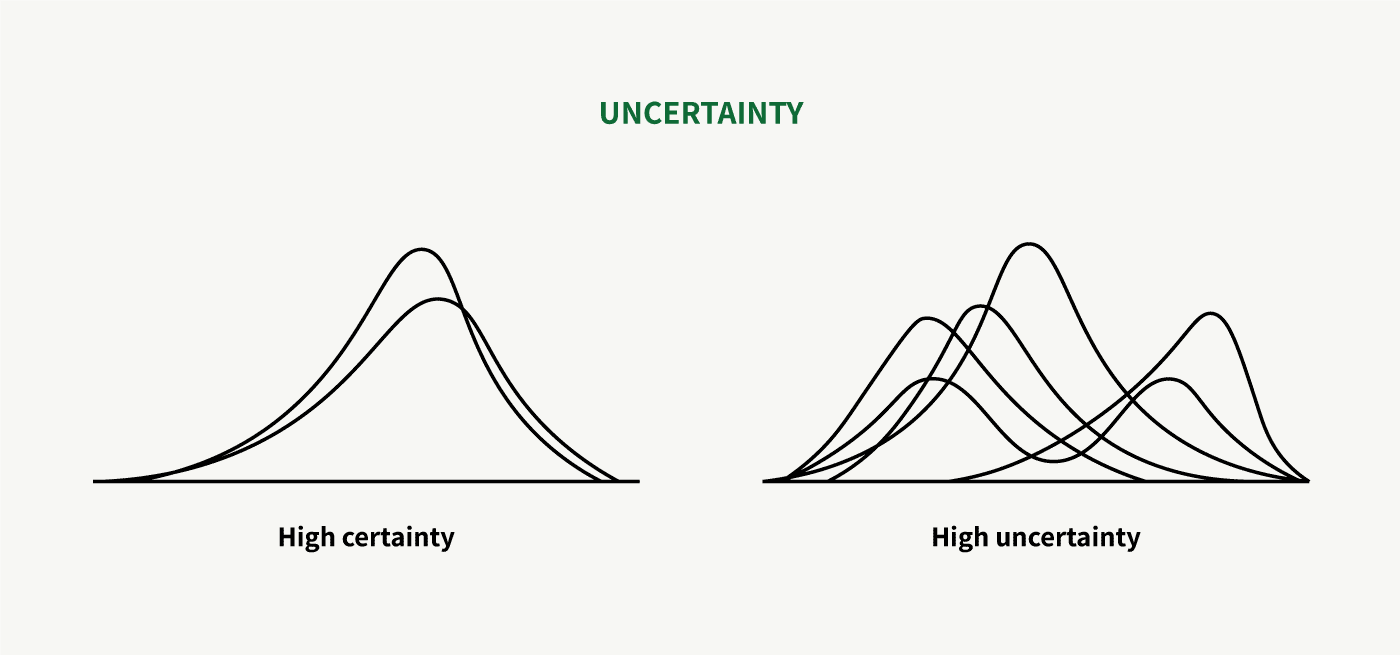
The uncertainty of a system essentially depends on two factors: its complexity and your understanding.
A dice roll experiment is a simple, isolated system. Forecasting interest rates—which are influenced by millions of external, dynamic variables—is a complex system. In the latter case, your understanding of the system matters little in terms of its uncertainty. But when you deal with something that is somewhere between these extremes, you can mitigate or remove uncertainty by increasing your understanding of the system. The more you move away from complexity, the more your understanding of it matters, and the better you understand something, the less uncertain it becomes.
For example, in macro investing, your understanding of the subject matter can only do so much for you because almost all parts of the macro system are complex. The stock market in its entirety is a complex system as well. In complex systems, cause and effects are only detectible in hindsight. History has continued to show that the stock market is ever-changing and stubbornly defies prediction.
But that doesn’t mean uncertainty is eliminated if you do bottom-up investing. Some businesses, such as commodity-intensive businesses, are more prone to uncertainty than others. For example, if you deal with an oil-producing business, the range of outcomes for the primary driver of valuation is highly uncertain, no matter your general understanding of the oil market. The same goes with highly innovative companies where the existence of a future market or the competitive position for the product is questionable.
On the other hand, boring companies are easy to understand and generally operate simple systems. The range of future outcomes are relatively easy to predict. But because they are so, you rarely find a situation where the risk is skewed to the upside, except for uncommon situations in which the entire market is underpriced like in the bottom of the financial crisis.
Now on to the definition of risk: What does “risk skewed to the upside” mean?
Risk is what you see once you, with a degree of certainty, can define the range of future outcomes, i.e. the probability distribution. And like uncertainty, you can think of risk as existing on a spectrum.
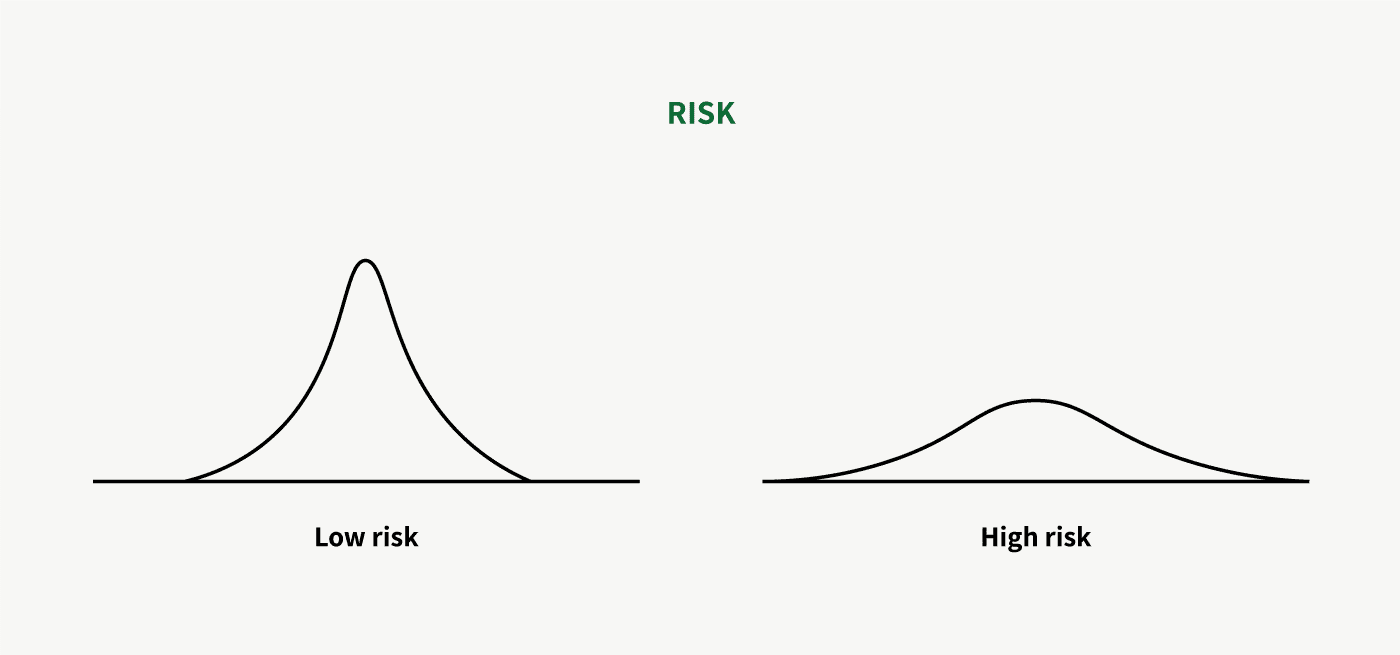
No future outcome for any investment is a sure thing. The future for every business, whether boring or cutting-edge, exists somewhere on a probability distribution as shown above. Absent the impact of stock prices, the variance of the future outcome represents the investment’s risk. (To be clear, this is business risk, not volatility.)
Here’s the counterintuitive point: In investing, what you want to do is eliminate uncertainty and be generally agnostic about risk.
Every investment contains a level of risk which you cannot eliminate. But it shouldn’t matter much whether the distribution of future outcomes is narrow or wide. You account for that in your position size. The only important thing you want to care about in terms of risk is whether you can define it and where it’s skewed. The beauty of investing lies in asymmetries.
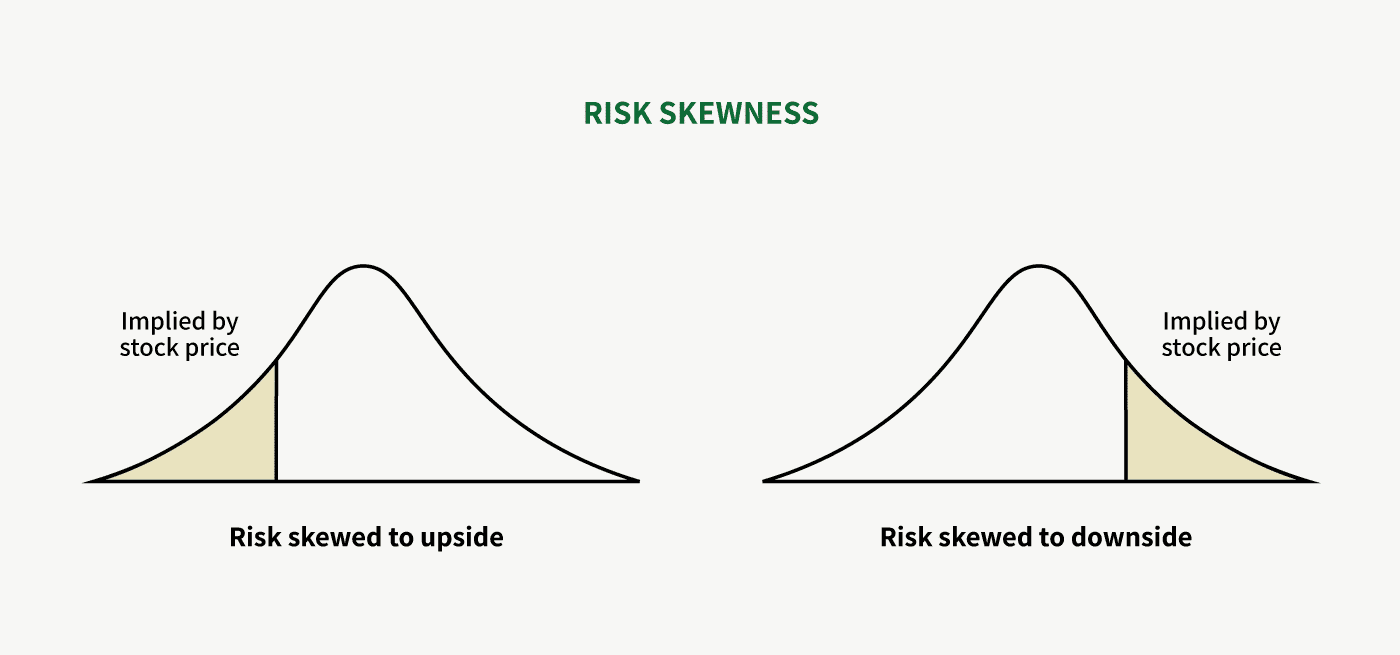
The nature of the stock market’s pari-mutuel system is that not many opportunities like these will show up where you have a lot going for you: where you have a lot of certainty, where you understand the business well enough to define the range of future outcomes, where you can value the business well, and the risk is largely skewed to the upside. It’s when you’ve got all these factors working at once that you know when to play the pari-mutuel system.
Conclusion
The mental models of the pari-mutuel system and Knightian uncertainty are invaluable thinking tools for the investor. It’s when you understand these mental models that you realize why not all great companies make for great investments and why investing isn’t easy.
But in order to play the game of active investing right, you only have to follow a few important rules:
- Invest like a pari-mutuel bettor
- Remove uncertainty by focusing on non-complex systems and staying within your circle of competence
- Bet big and bet seldom when the odds are heavily in your favor and the risk is skewed to the upside


