In times where fear of an epidemic arising from the spread of a Coronavirus originating in China gains traction around the world on the verge of panic from a social and economic standpoint, I think it makes sense to take a look at the issue of epidemics from a mathematical and theoretical perspective.
We’ll revisit the epidemic models mainly used by epidemiologists to predict the course of infection and mortality.
While epidemic models are great at explaining mostly spreading of diseases in a biological setting, like diseases, they are also great mental models for explaining how herd-behavior can occur out of small inflections in various other domains. For example, using epidemic models to understand transmission of attitude can be used to comprehend the feedback mechanisms that support speculative financial bubbles or religious/political propaganda.
And because feedback mechanisms are near omnipresent occurrences in financial markets, it makes a great deal of sense for any investor to understand the structure behind the powerful mental lens of how epidemics occur.
We’ll let Nobel-prize winning economist Robert Shiller explain epidemic models in their basic form from the book, Irrational Exuberance:
In the simplest epidemic models, it is assumed that the disease has a given infection rate (the rate at which the disease spreads from contagious people to susceptible people) and a given removal rate (the rate at which infected people become no longer contagious, through recovery or death).
So in its basic form, epidemics occur as a relationship between two factors: the infection rate and the removal rate.
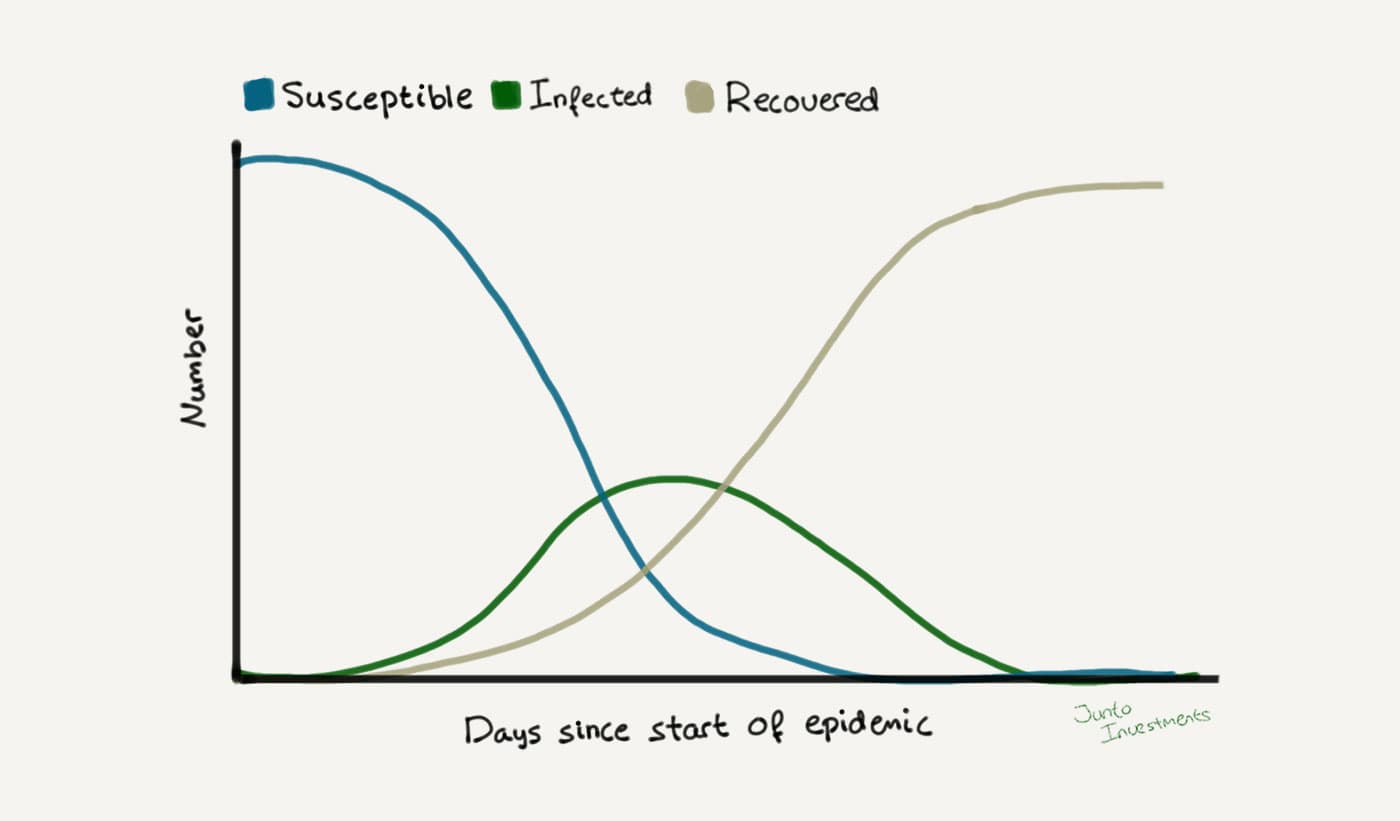
As an infection rate is discovered, three instances can occur.
- If the removal rate of the infection is zero, the epidemic follows a logistical curve. Initially, the percentage of the population that is infected rises with the infection rate. The rate of increases begins to decline as the number of potential infections (the pool of yet-to-be-infected susceptibles) begins to be depleted. When the entire population is infected, the logistical curve becomes flat.
- If the removal rate is greater than zero but less than the infection rate, the epidemic will be bell-shaped and can peak before 100% of the population is infected (illustrated above).
- Lastly, if the removal rate is greater than the infection rate, the epidemic will never gain traction and the epidemic is flat.
From this observation we can quickly infer that epidemics are closely related and sensitive to what best-selling author Malcolm Gladwell calls the tipping point; the moment of critical mass, the threshold, the boiling point. In his book, he elaborates:
“Look at the world around you. It may seem like an immovable, implacable place. It is not, With the slightest push — in just the right place — it can be tipped.”
In terms of epidemics, the tipping point works both ways. As Shiller explains:
… if the removal rate is just above the infection rate, then a nearly healthy population is in danger of an epidemic, for any small uptick in the infection rate or downtick in the removal rate can tip the balance toward a new epidemic.
And because the repercussions of the bell curve if the removal rate is greater than zero but still lower than the infection rate, time to up the removal rate is a crucial matter.
Thus, epidemiologists can infer that a change in weather patterns that will tend to keep people indoors together (where they are more likely to infect one another) may cause the infection rate to increase above the removal rate. The epidemic will then begin, but the absolute number of infectives will grow slowly at first. If, in this example, the weather changes fairly soon again in such a way that the infection rate is brought back down, so that the number of infectives never becomes very large, then the epidemic will fail to be noticed by the general public. But if the bad weather lingers long enough relative to the difference between the bad-weather-infection rate and the removal rate, then the epidemic will become large and noticeable in the population at large.
Now, how does this relate to financial markets?
Word-Of-Mouth Transmission of Ideas in Financial Markets
Although not as rigid as in biological domains, the same idea behind epidemic models can be applied to several other domains involving human behavior.
In the case of transmission of ideas, the infection rate is the communication of the idea, while the removal rate occurs by forgetting or losing interest.
The reason why epidemic models are less constant outside the field of biology as applied to e.g. financial markets is mainly due to the evidence of communication loss and distortion; what Claude Shannon called equivocation. Because transmitting ideas with just the slightest complexity from person to person is likely to become unreliable at a certain link, the accuracy of transmitting ideas leading to an epidemic is likely to falter before it reaches the entire population. But the effects can still be huge.
So despite this equivocation, thinking in terms of epidemic models is still invaluable in understanding the kind of things that can bring about changes in market prices of financial assets. As evident, word-of-mouth is tough to beat, especially when there is a vivid, tellable story about an event that can be passed on to others. The fairy tale stories around every internet stock in the late ’90s leading to a large speculative bubble of an entire market is an example. Marketers know that rapid, positive word-of-mouth is the holy grail in their domain. Ponzi schemes feed on it.
The idea is: As infection rate is above removal rate, the longer that relationship persists, the larger the marginal increase of “infecting” the potential population will be. If it persists long enough to gain traction, it can ultimately lead to large epidemics and speculative bubbles, whether in single assets or entire markets.


